Units & Measurements
		Standards and Units		Dimensional Analysis »

Units & Measurements - 01

Standards and Units

Base (Fundamental) and Derived Units

Table 1: The fundamental SI units
Base Quantity	Unit	Symbol
length `l`	meter	m
mass `m`	kilogram	kg
time `t`	second	s
temperature `T`	kelvin	K
electric current `I`	ampere	A
amount of substance	mole	mol
luminous intensity	candela	cd

Physical quantities can be divided into two categories: base (fundamanetal) quantities and derived quantities. The corresponding units for these are called base units and derived units.

The base units cannot be expressed in terms of further simpler quantities/units. There are seven base quantities/units in the SI system.

Table 2: Some derived SI units
Derived Quantity	Unit
area `A`	m²
volume `V`	m³
density `ρ`	kg/m³
speed `v`	m/s
acceleration `a`	m/s²
force `F`	kg m/s² or N
pressure `p`	N/m²
energy `E`	N m or J
power `P`	J/s or W

There are further two supplementary SI units for angle and solid angle—the radian (rd or ^c) and the steradian (sr) respectively.

Derived quantities are those physical quantities which can be expressed in terms of combinations of base quantities. Some examples of derived quantities are given in Table .

The radian measure

Fig 1: Angle of 1 radian. (Source: Wikipedia 2010, Radian)

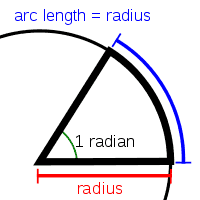
The radian is defined as the angle subtended at the centre of a circle by an arc whose length is equal to the radius of the circle. For any angle subtended at the centre of a circle (denoted by θ in radians), if l is the length of the arc, and r the radius of the circle, then

$θ = \frac{l}{r} \Rightarrow l = r θ$

.......(1)

One complete revolution of a circle encircles $2 π radians$ . Thus,

$2 π radians = 360 °$

.......(2)

Unit Prefixes

In the metric system, the larger and smaller units are defined in multiples of 10 from the standard unit, and this makes calculation particularly easy.

Table lists some standard unit prefixes used in physics for the SI system.

Table 3: Some prefixes for SI units
Power	Prefix	Symbol
1,000,000,000 = 10⁹	giga-	G
1,000,000 = 10⁶	mega-	M
1,000 = 10³	kilo-	k
100 = 10²	hecto-	h
10 = 10¹	deka-	da
0.1 = 10⁻¹	deci-	d
0.01 = 10⁻²	centi-	c
0.001 = 10⁻³	milli	m
0.000001 = 10⁻⁶	micro-	µ
0.000000001 = 10⁻⁹	nano-	n
0.000000000001 = 10⁻¹²	pico-	p

Some practical units used in physics

for lengths

Angstrom (Å): For measuring distances at par with atomic sizes.
$1 Å = 10^{- 10} m$
Astronomical unit (AU): The mean distance between the sun and earth.
$1 AU = 149.6 million km$
Light year (ly): The distance travelled by light in one year.
$1 ly = 9.467 \times 10^{12} km = 6.3 \times 10^{4} AU$

for mass

Atomic Mass Unit (amu or u): Defined as 1/12^th the mass of one ${}_{6}^{12}C$ (carbon-12) isotope.
$1 amu = 1 u = 1.66 \times 10^{- 27} kg$
Quintal (q):
$1 q = 100 kg$
Tonne (metric ton) (t):
$1 t = 1000 kg$

for area

Acre :
$1 acre = 4047 m^{2}$
Hectare :
$1 hectare = 10^{4} m^{2}$

Unit conversions

Length units

$\begin{array}{l} 1 in. = 2.54 cm \\ 1 ft = 0.3048 m \\ 1 m = 39.37 in. \end{array}$

$1 mi. = 5280 ft = 1.609 km = 8 / 5 km$

Volume units

$\begin{array}{l} 1 cc = 1 {cm}^{3} = 1 mL \\ 1 L = 1000 {cm}^{3} \end{array}$

Pressure units

$\begin{array}{l} 1 bar = 10^{5} N m^{- 2} = 10^{5} Pa \\ 1 atm = 760 mm Hg = 1.013 \times 10^{5} N m^{- 2} \end{array}$

Energy units

$\begin{array}{l} 1 cal = 4.186 J \\ 1 J = 10^{7} ergs \\ 1 kWh = 3.60 \times 10^{6} J \end{array}$

Power units

$1 hp = 0.746 kW$

Solved Examples

The density of one kind of steel is

8.25 g ​ / ​ {cm}^{3}

. Expressed in SI units, this is
(a)

0.825 kg ​ / ​ m^{3}

(b)

825 kg ​ / ​ m^{3}

(c)

8250 kg ​ / ​ m^{3}

(d)

82, 500 kg ​ / ​ m^{3}

(Rex & Wolfson 2010, Physics, p. 15 #12)

The unit for density has to be converted from $g / {cm}^{3}$ to $kg / m^{3}$ .

\begin{array}{l} 8.25 g ​ / ​ {cm}^{3} = 8.25 \times 1 \frac{g}{{cm}^{3}} = 8.25 \times \frac{(1 g)}{{(1 cm)}^{3}} \\ = 8.25 \times \frac{(1 \times 10^{- 3} kg)}{{(1 \times 10^{- 2} m)}^{3}} = 8.25 \times \frac{10^{- 3}}{{(10^{- 2})}^{3}} \times \frac{(1 kg)}{{(1 m)}^{3}} \\ = 8.25 \times 10^{- 3 - (- 6)} \times 1 \frac{kg}{m^{3}} = 8.25 \times 10^{3} kg ​ / ​ m^{3} = 8250 kg ​ / ​ m^{3} \end{array}

▼(show solution)

A car is speeding down the road at 85 mph (miles per hour). In SI units, this would be
(a)

38 m ​ / ​ s

(b)

40 m ​ / ​ s

(c)

42 m ​ / ​ s

(d)

44 m ​ / ​ s

(Adapted from: Rex & Wolfson 2010, Physics, p. 15 #13)

The conversion from mph to kmph would go like this:

\begin{array}{l} 85 mph = 85 \times \frac{1 mi.}{1 h} = 85 \times \frac{(\frac{8}{5} \times 1000) m}{3600 s} \\ = \overset{17}{85} \times \frac{\overset{2000}{8000}}{5} \times \frac{1}{\underset{900}{3600}} \frac{km}{s} = \frac{340}{9} m ​ / ​ s \\ = 37 \frac{7}{9} m ​ / ​ s \approx 38 m ​ / ​ s \end{array}

▼(show solution)

The average distance of the Sun from the Earth is 390 times the average distance of the Moon from the Earth. Now consider a total eclipse of the Sun (Moon between Earth and Sun; see figure) and calculate (a) the ratio of the Sun's diameter to the Moon's diameter, and (b) the ratio of the Sun's volume to the Moon's volume.
Resnick_Halliday_&_Krane_2002_Physics_vol_1_p_12_2.png

Resnick_Halliday_&_Krane_2002_Physics_vol_1_p_12_2.png

3.82 \times 10^{5} km

, what is the diameter of the Moon? (Adapted from: Resnick, Halliday & Krane 2002, Physics vol 1, p. 12 #2)

(a) By similar triangles, the ratio of the Sun-Earth distance and the Moon-Earth distance is the same as the ratio of the diameters of the Sun and the Moon. Thus, 390:1 is the ratio of their diameters.

(b) Now that we know the ratio of diameters of the Sun and the Moon, and volume of a sphere ( $\frac{4}{3} π R^{3}$ ) is proportional to the cube of the radius (or diameter), the ratio of their volumes is 390³:1.

(c) If we consider the Moon's distance (r) as the radius of a 'great circle' with center at the observer's position on the Earth, and the diameter (D) of the moon approximating the length of the arc of the 'great circle' which subtends and angle of 0.52°, then,

$\begin{array}{l} D = r θ = (3.82 \times 10^{5} km) \times (0.52 \times \frac{π}{180} radians) \\ = \frac{3.82 \times 10^{5} \times 0.52 \times 22}{180 \times 7} km \approx 3500 km \end{array}$

▼(show solution)

Earth s equatorial radius is 6378 km. A spacecraft is in circular orbit 100 km above the equator. If the spacecraft orbits every 86.5 minutes, what's its speed in kmph? (Adapted from: Rex & Wolfson 2010, Physics, p. 15 #39)

The radius of the orbit of the spacecraft:

R = (6378 + 100) km = 6478 km

The length of the orbit (circumference) $= 2 π R = 2 π \times 6478 km$

Time taken to complete one orbit $= 86.5 min = \frac{86.5}{60} h$

Thus, speed:

= \frac{distance}{time} = \frac{2 \times \frac{22}{7} \times 6478}{\frac{86.5}{60}} = \frac{2 \times 22 \times 6478 \times 60}{7 \times 86.5} = 28, 244 kmph

▼(show solution)

Feedback Form▼(open form)

List of References

Resnick, R, Halliday, D & Krane, KS, Physics, vol. 1, 5th edn, NY, USA: John Wiley & Sons, 2002.

Rex, AF & Wolfson, R, Essential College Physics, 1st edn, NY, USA: Pearson Addison-Wesley, 2010.

Tipler, PA & Mosca, G, Physics for Scientists and Engineers with Modern Physics, 6th edn, NY, USA: W. H. Freeman, 2008.

Wikipedia contributors, 'Radian,' Wikipedia, The Free Encyclopedia, viewed 06 December, 2010 <http://en.wikipedia.org/wiki/Radian>, 2010.

Bibliography

Arora, SL, New Simplified Physics – A Reference Book for Class XI, 8th edn, New Delhi, India: Dhanpat Rai & Co., 2019.

Young, HD & Freedman, RA, Sears and Zeemansky's University Physics with Modern Physics, 13th edn, CA, USA: Pearson Education, 2012.

		Standards and Units		Dimensional Analysis »
Units & Measurements

Standards and Units

Units & Measurements - 01

Standards and Units

Base (Fundamental) and Derived Units

The radian measure

Unit Prefixes

Some practical units used in physics

for lengths

for mass

for area

Unit conversions

Length units

Volume units

Pressure units

Energy units

Power units

Solved Examples

Feedback Form▼(open form)

List of References

Bibliography

Monographs TOC

Compendium TOC