
 Units & Measurements Units & Measurements |
|||||
| Significant Figures | System of Units |
Units and Measurements - 02
Significant Figures
Numbers, Accuracy and Precision
There are two types of numbers.
- Exact numbers are numbers that we get from counting, or those which come from definitions. They are taken to be absolutely accurate. For e.g., (i) the count: 47 people in a hall, or (ii) the definition: 1 inch = 2.54 centimeters.
- Inexact numbers result from measurements. All measurements of physical quantities are not exact – they have built-in estimates. The accuracy of a measured value depends on the limits of the experimental uncertainty. The value of this uncertainty depends on (a) the quality of the measuring device, (b) the skill of the experimenter, and (c) the number of measurements performed.
The accuracy of a measurement indicates how closely it agrees with the correct value. On the other hand, precision indicates how closely each measurement (in a group of repeated measurements) agrees with one another. It is possible that a measurement be quite precise yet quite inaccurate due to an error inherent in each process of measurement (for e.g., as can happen in the case of a faulty balance). Thus, the reliability of a measuring instrument affects the accuracy of a measurement.
To improve accuracy and precision, measurements are often repeated to arrive at average values. Average values thus obtained are usually more reliable than individual measurements.
Significant Figures
In a measurement, the number of digits believed to be correct (by a skillful person making the measurement) is the number of significant figures, or sig figs. In measurements, we include a maximum of one estimated digit, and no more.
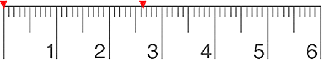
The general rule for estimation of the last digit is to record to th of the smallest division of the measuring device, but it can be greater, such as th, i.e. th. So, for the common centimeter-ruler, in which the smallest division is 1mm, the estimate for the last digit can be to 0.1mm or 0.2mm, depending on the whether the experimenter feels comfortable with recording to th, or th of the smallest division.
Suppose a student records a length of 26.2mm with a ruler (between the red marks in Fig. ). In his/her judgment, the length is greater than 26.1mm but less than 26.3mm, and the so the best estimate is 26.2mm. The measurement can be written as . The number 26.2mm contains three significant figures. Although the last digit, 2, is an estimate, it is considered to be a significant figure for the measurement.
Rules governing significant figures
Identifying significant digits
The following rules are helpful in identifying significant digits: (Whitten et al 2004, Chemistry, pp. 23-5)
- Digits other than zero are significant.
e.g., 40.1m has 3 sig figs.
- Zeroes are sometimes significant, and sometimes they are not.
- Zeroes at the beginning of a number (used just to position the decimal point) are not significant.
e.g., 0.025m has 2 sig figs. In scientific notation, this can be written as .
- Zeroes between nonzero digits are significant.
e.g., 40.1m has 3 sig figs
- Zeroes at the end of a number that contains a decimal point are significant.
e.g., 41.0m has 3 sig figs, while 441.20m has 5. In scientific notation, these can be written respectively as and .
- Zeroes at the end of a number that does not contain a decimal point may or may not be significant. If we wish to indicate the number of significant figures in such numbers, it is common to use the scientific notation.
e.g., The quantity 52800km could be having 3, 4, or 5 sig figs—the information is insufficient for decision. If both of the zeroes are used just to position the decimal point (i.e., the number was measured with estimation ), the number is (3 sig figs) in scientific notation. If only one of the zeroes is used to position the decimal point (i.e., the number was measured ), the number is (4 sig figs). If the number is , it implies (5 sig figs).
- Exact numbers can be considered as having an unlimited number of significant figures. This applies to defined quantities too.
e.g.,
- The rules of significant figures do not apply to (a) the count of 47 people in a hall, or (b) the equivalence: 1 inch = 2.54 centimeters.
- In addition, the power of 10 used in scientific notation is an exact number, i.e. the number 103 is exact, but the number has 1 sig fig.
It actually makes a lot of sense to write numbers derived from measurements in scientific notation, since the notation clearly indicates the number of significant digits in the number.
Arithmetic with significant figures
Addition and Subtraction
In addition and subtraction, the answer can’t have more digits to the right of the decimal point than in either of the original numbers. Rounding is done as appropriate. Note that the number of significant figures can change during these calculations. e.g.,
Multiplication and Division
In multiplication and division, an answer contains no more significant figures than the least number of significant figures used in the operation. e.g.,
Combined calculations
In combined calculations, which involve both addition/subtraction and multiplication/division, the rules for identifying significant digits must be applied before, and after, each calculation stage involving addition or subtraction. e.g.,
List of References
Bibliography
| Significant Figures | System of Units | ||||
 Units & Measurements Units & Measurements |
 High School
High School Mathematics
Mathematics Sets & Basic Operations
Sets & Basic Operations