
 Units & Measurements Units & Measurements |
|||||
| Significant Figures | System of Units |
Units and Measurements - 01
Physical Quantities and Units
A physical quantity is any property of matter or energy that can be quantified, i.e. measured and expressed in numbers. For example, length, time, mass and temperature are physical quantities.
A measurement is a precise value which expresses "how much." How much of what depends upon what is being measured. All measurements need units. Without a unit, a measurement has no meaning.
A unit is a specific quantity designated as a standard against which other measurements of the same kind are made. The standard unit for length is the meter. When a car is said to be "5 meters" long, it means that the car is five times as long as the standard length of "1 meter".
So, a measurement has two parts, a numerical quantity and a unit. The numerical quantity specifies how many times the unit is contained in the measurement. Thus, for the length measurement of 5 meters for the car, the unit meter is contained five times in the length of the car.
The choice of a unit is based on certain requirements. They are:
- The unit should be capable of being precisely defined, so that there is no ambiguity.
- The unit should be easily reproducible, so that copies (secondary standards) can be easily created in other laboratories for reference purposes.
- The unit should be independent of the time and place of measurement.
The units are generally written abbreviated as symbols. For example, one set of names and symbols of units of mass, length, and time are kilogram (kg), meter (m) and second (s). It should be noted that for both the unit and its symbol, the plural form is not used for measurement greater than unity. Thus, the length of the car is 5 meter, or 5m, and not 5 meters or 5 ms. Moreover, small letters are used for the units and the symbols, except when the name of the unit is derived from a proper name, in which case the symbol (only) is written with capital letter. Thus, one unit of force named after the scientist Isaac Newton is written as newton (N).
Fundamental quantities, or base quantities, are those physical quantities which are independent of each other, and so cannot be expressed in terms any other. The units of these quantities are called the fundamental units or base units.
System of Units
The Metric System (MKS System)
The French were instrumental in coming up with the Metric System, where the three common fundamental units are the meter (m) for length, the second (s) for time, and the kilogram (kg) for mass. This system of measurement is also known as the MKS system (for Meter, Kilogram and Second). However, we will begin exploring units with the fundamental unit for temperature.
Unit of temperature
Temperature is the measure of the degree of "hotness" or "coldness" of a body. When two bodies are in contact, heat flows from the body at higher temperature to the one at lower temperature. If heat does not flow, the bodies are considered to be at a thermal equilibrium.
Thermometers are devices used to measure the temperature of an object. Common thermometers use changes in the volume of a liquid (observed as the height of a liquid in a narrow sealed capillary tube) with rise in temperature to make calibrations for measuring temperature.
Earlier, water or water-alcohol mixture were used as the thermometric liquids, but the non-uniform changes in volume of water with temperature rise was a problem.
The fahrenheit scale
In 1714, the physicist Daniel Fahrenheit introduced mercury as the thermometric liquid. Mercury had the following advantages over water: (i) undergoes uniform volumetric change with temperature, (ii) it does not wet glass, and (iii) it has a lower freezing point and a higher boiling point than water, leading to a wider range of temperature measurements.
Fahrenheit chose the term degree (symbol °) for the unit of temperature, which came to be known as the fahrenheit degree (°F). He then decided to have 180 such "degrees" between the freezing temperature and the boiling temperature of water. To fix the 0°F on the fahrenheit scale, he decided to mark it as the coldest temperature he could obtain in his lab by mixing ice with salts to make it colder. Fixing 0°F at this temperature resulted in the normal freezing point of water being 32°F, with 212°F (by adding 180°F) being the normal boiling point of water. Thus was born the fahrenheit temperature scale.
The celsius (centigrade) scale
In 1742, the astronomer Anders Celsius proposed a temperature scale in which the normal freezing and boiling points of water were to be 100 "degrees" apart. This unit of temperature was the centigrade degree (°C), later renamed to celsius degree. Thus, each degree celsius is 9/5 times larger than each degree fahrenheit. The normal freezing point of water was set at 0°C, and so the normal boiling point of water became 100°C.
The Kelvin scale
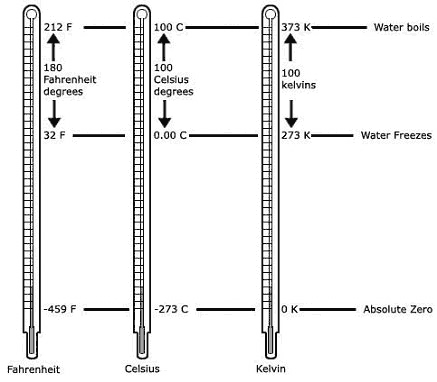
In 1848, Lord Kelvin said that −273°C is the lowest possible temperature, which he termed absolute zero. He suggested a temperature scale wherein its zero would correspond to this absolute zero, with the temperature units identical in size to the celsius scale. This scale came to be known as the Kelvin scale or the absolute temperature scale, and the temperature units are known simply as kelvins (K). The normal freeing and boiling points for water on the kelvin scale are 273K and 373K respectively.
A comparison of the three temperature scales is given in Fig. .
Unit of time - the second
Since the dawn of civilization, the measurement of time was linked to the heavens. The revolution and rotation of the earth provided convenient references for choosing the two broad divisions of time – the year and the day/night cycle. When the sun was at its highest in the sky (when the length of shadow cast by a vertical pole is the shortest), the moment was defined as noon, and the interval between one noon and the next became a solar day.
The Egyptians divided the year into 365 solar days, the time taken by earth to complete one orbit around the sun. The Babylonians divided a solar day (day+night) into 24 divisions now called hours. They further subdivided each hour into 60 divisions we know as minutes, and each minute into 60 divisions we know as seconds. The Babylonian civilization attached mystical importance to multiples of 12, which resulted in the divisions for hours, minutes and seconds as we know today.
Since the duration of the solar day is not uniform throughout the year, the average of the solar days for an entire year was calculated to arrive at the mean solar day, which, from 1889, was taken as a unit of time measurement for defining the further sub-divisions. 1/24th of the mean solar day thus became the standard hour.
Unit of length - the meter
In 1790, the meter was defined as one ten-millionth of the distance from the North Pole to the equator along the prime meridian.(See Fig. )
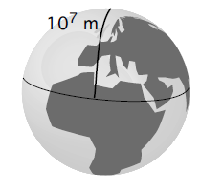
However, improved measurements made in the 19th century of the length of the prime meridian indicated that the standard meter actually was a little shorter than the meridian-based calculation. Instead of redefining the unit of length and forcing everyone to change to the new more accurate length, it was decided to keep the earlier standard length and discard the definition of the meter linked to the prime meridian.
Thus, in 1875, the standard unit of length was indicated on a platinum-iridium bar (kept at 0°C at the Bureau of Weights and Measures at Sevres, near Paris) as the distance between two scratches designating a length of one meter.
Unit of mass – the kilogram
Anything that takes up space is called matter. Mass is the measure of the amount of matter in an object. In 1790, with the objective of relating length with mass, the standard unit of mass, the kilogram, was defined as the mass of water at 4°C (when water has the maximum density) in a cube whose side was 1/100th of the standard meter.
In 1875, the standard kilogram (as maintained since 1790) was used as a reference to fashion out a cylinder of the same weight (in vacuum) from the platinum-iridium alloy, as the new standard of mass, and kept at Sevres, near Paris.
The International System of units (SI System)
The S.I. system of units is refinement and extension of the metric system. It was adopted in 1960 by most countries.
Unit of temperature – the kelvin
The kelvin has been officially adopted by the SI system for measuring temperature. However, the Celsius scale is still more common in use.
Unit of time - the second
With the coming of the atomic clock, it was sought to decouple the definition of the units of time from movements of the earth. In 1967, the second was defined as the amount of time it takes for a cesium-133 atom to vibrate 9,192,631,770 times.
Once again, similar to the case for the unit of length (the meter), the existing standard (since 1887) for the second was used to determine the number of vibrations needed by the cesium-133 atom to cover the duration of a second, and the new definition was drawn up to completely shift the definition of the unit of time to the unvarying vibrational property of the atom.
Unit of length - the meter
In 1960, the meter was redefined as 1,650,763.73 wavelengths in a vacuum of the orange-red line of the spectrum of krypton-86. The advantages of this definition were two-fold. Firstly, since the "1,650,763.73 wavelengths" corresponded to the existing standard of the meter based on the platinum-iridium bar, the earlier established standard could be continued. Secondly, the need to keep a physical object to serve as standard under a particular temperature was no longer needed, since the new definition could be replicated in any equipped laboratory.
Using the standard of meter, the speed of light in vacuum was found to be 299,792,458 m/s, and this value was defined and adopted as standard for light speed.
In 1983, a further redefinition of meter was effected using the speed of light as the base. The meter was now defined as the distance traveled by light in vacuum during a time interval of 1/299,792,458 of a second.
Needless to say, this again was just a redefinition of the prevailing standard for the meter – it just made it easier for the laboratories to replicate the standard. Note that the new definition now depends upon the definition of the second, which had been formalised in 1967 and is based on the vibration of the cesium-133 atom.
Unit of mass – the kilogram
The definition of unit of mass, the kilogram, was adopted in 1875. It was the only remaining SI unit, the definition of which is linked to a physical object. But there are problems associated with maintaining a physical object to define a standard, since contamination and/or degradation may alter the standard over time.
Finally, the definition of the unit of mass was delinked with a physical object. The new definition involves accurate weighing machines called 'Kibble balance', which uses Planck's Constant to measure the mass of an object using a precisely measured electromagnetic force.
| Year | Unit of length (meter) | Unit of time (second) | Unit of mass (kilogram) |
|---|---|---|---|
| 1790 | meter defined as one ten-millionth of the distance from the North Pole to the equator along the prime meridian. | kilogram defined as mass of water at 4°C in a cube whose side was one-hundredth of the standard meter. | |
| 1875 | meter redefined as the distance between two marks on a platinum-iridium bar (kept at 0°C at at Sevres, near Paris). | kilogram redefined as the mass of a platinum-iridium alloy cylinder (kept in vacuum at Sevres, near Paris). | |
| 1889 | second defined as 1/86400th of the mean solar day. | ||
| 1960 | meter redefined as 1,650,763.73 wavelengths in a vacuum of the orange-red line of the spectrum of krypton-86. | ||
| 1967 | second redefined as the time it takes for a cesium-133 atom to vibrate 9,192,631,770 times. | ||
| 1983 | meter redefined as the distance traveled by light in vacuum during a time interval of 1/299,792,458 of a second. | ||
| 2019 | kilogram redefined on the basis of Planck's constant, measured using the Kibble balance. |
Other SI Fundamental Units
| Physical Quantity | SI Unit | |
|---|---|---|
| Length | : | meter (m) |
| Mass | : | kilogram (kg) |
| Time | : | second (s) |
| Temperature | : | kelvin (K) |
| Electric Current | : | ampere (A) |
| Luminous Intensity | : | candela (cd) |
| Amount of Substance | : | mole (mol) |
Apart from the units for time (the second), length (the meter), mass (the kilogram) and temperature (the Kelvin), the SI system of units has three more fundamental units for measuring electric current (the ampere), the amount of substance (the mole) and luminous intensity (the candela). All the fundamental SI units are listed in Table .
These other fundamental units will be dealt with later within their respective subject areas.
Derived Units & Quantities
Derived units are those units whose definitions are based on the fundamental units. Thus, the seven fundamental SI units are used to derive many other units for physical quantities, such as for area and volume. Such quantities are called derived quantities.
Area, which is a measure of the size enclosed by a closed line on a surface, can be simply illustrated by a rectangular figure having a length l and a breadth b. The area of the rectangle is . Since each of these has the unit of meter, the unit of area becomes or , read as square meters.
Volume is the amount of space occupied by an object, which can be illustrated by a cube with a length l, a breadth b, and a height h. The volume of the cube is . Since each of these has the unit of meter, the unit of volume becomes , read as cubic meters.
Non-SI units used with the SI
Some non-SI units have been accepted as partners of the SI units. The common ones are those related to the quantities Time and the Plane Angle.
Time
The non-SI units related to time are:
- minute (min) [1min = 60s]
- hour (h) [1h = 60min = 3600s]
- day (d) [1d = 24h = 86400s]
Plane Angle
A degree of arc (or simply a degree, symbol °) is a plane angle which represents of a full rotation along the circumference of a circle. This system of measurement has its roots in the Babylonian era. Further subdivisions of a degree are:
- minute ( ' ) [ 1' = (1/60)° ]
- second ( " ) [ 1" = (1/60)' = (1/3600)° ]
Supplementary SI Units
There are two supplementary SI units, which have been now included under the category of derived units. These are the radian (for measuring plain angle) and the steradian (for measuring solid angle at center of a sphere) The latter will not be covered now.
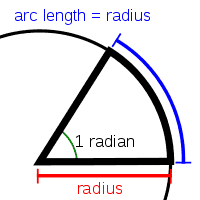
Unit of Angle – the radian
The radian (rd or c) is the unit of angular measurement. It is defined as the angle subtended at the centre of a circle by an arc whose length is equal to the radius of the circle (Fig. ).
Thus, for any angle subtended at the centre of a circle (denoted by in radians), if s is the length of the arc, and r the radius of the circle, then
Considering the entire circumference of a circle as the arc,
Thus, one complete revolution of a circle encircles . This means that
British System (FPS system)
The British system of units came into being over many years in a non-planned way. Units such as second (for measuring time), pound (for weight) and foot (for length) are part of the British system. As of today, except for Myanmar, Brunei, Yemen and the United States, all other countries (including Britain) have shifted to the metric system of units. The British system is also known as the FPS System.
All measurement systems are based on arbitrary standards. The SI system is as arbitrary as the British system, however, the relationships between the units are more systematic and easy to remember.
The CGS System
The CGS system is an earlier version of the metric system in which the unit of length is the centimeter (cm)—1/100th of a meter—, the unit of mass is the gram (g)— 1/1000th of a kilogram—, and the unit of time is the second(s). Although superseded by the MKS/SI system, it is still used is some subject areas.
The Scientific Notation
| Power | Prefix | Symbol |
|---|---|---|
| 1,000,000,000 = 109 | giga- | G |
| 1,000,000 = 106 | mega- | M |
| 1,000 = 103 | kilo- | k |
| 100 = 102 | hecto- | h |
| 10 = 101 | deka- | da |
| 0.1 = 10-1 | deci- | d |
| 0.01 = 10-2 | centi- | c |
| 0.001 = 10-3 | milli | m |
| 0.000001 = 10-6 | micro- | µ |
| 0.000000001 = 10-9 | nano- | n |
| 0.000000000001 = 10-12 | pico- | p |
The scientific notation, exponential notation, or the standard notation involves writing a number as a product of two numbers, the first, called the base, is a value from 1 to 10 (including decimals), while second is a power of 10, (positive or negative). The power to which 10 is raised is called an exponent. Here are a few examples of numbers written in the scientific notation:
Prefixes in the SI/Metric System
Now that the units are defined, larger/smaller units for the same physical quantities have been introduced in the metric and SI systems by multiplying/dividing the units by powers of 10. The names of the new units are derived by adding a prefix to the name of the unit. For a list of the common prefixes, see Table .
For example, the prefix "kilo-," abbreviated as k, denotes a unit larger by a factor of 1000; thus
1 kilogram = 1kg = 103 gram = 103g
List of References
Bibliography
| Significant Figures | System of Units | ||||
 Units & Measurements Units & Measurements |
 High School
High School Mathematics
Mathematics Sets & Basic Operations
Sets & Basic Operations